Im letzten Blogartikel haben Sie gesehen, dass Mathematik in besonderer Weise die begrenzten Ressourcen für unser System 2, für unser langsames, bewusstes und mit Aufmerksamkeitsfokussierung sowie geistiger Anstrengung verbundenes Denken, beansprucht. Wir alle erleben regelmäßig, dass unsere Ressourcen für dieses Denken tatsächlich sehr begrenzt sind. Auch in einer ruhigen Umgebung mit wenig ablenkenden Reizen können wir uns kaum mehr als 7 Zahlen auf einmal merken – wie also ist es den Mathematikern gelungen, so eine komplexe Wissenschaft aufzubauen? Wie im vorherigen Blogartikel kann ich nur einen kleinen Einblick in diese Frage geben, der in diesem Beitrag auf die mathematischen Darstellungen fokussiert.
Darstellungen verringern geistige Anstrengung: Funktion als expliziter Wissensspeicher
Am Anfang des letzten Blogartikels habe ich Sie aufgefordert \(13 \cdot 26\) im Kopf zu berechnen, was Sie mit etwas geistiger Anstrengung wahrscheinlich auch hinbekommen haben. Aber es gibt wohl nur wenige, die es schaffen, \(113 \cdot 226\) im Kopf zu berechnen. Dennoch lernen schon Grundschulkinder, wie man das Ergebnis dieser Multiplikation ohne Taschenrechner herausbekommt: Sie zerlegen das Problem und schreiben sich Zwischenergebnisse auf. So simpel das heute für uns klingt, war die Erfindung der Schrift auch für die Mathematik ein echter Durchbruch, um unsere begrenzten Ressourcen zu umgehen und unser Gedächtnis zu erweitern. Aber trotzdem lassen sich damit noch längst nicht alle Probleme überwinden. Wenn wir uns Zwischenergebnisse, Voraussetzungen oder gesuchte Größen aufschreiben, dann sind wir immer noch daran gebunden, dass wir eine Zerlegung des Problems finden, die es zulässt, dass für jedes Teilproblem nur so viele Informationen gleichzeitig berücksichtigt werden müssen, wie wir uns gleichzeitig merken und wie wir gleichzeitig verarbeiten können.
In der Einleitung zu diesem Artikel habe ich geschrieben, dass wir uns nur etwa sieben Zahlen auf einmal merken können – das war nicht ganz korrekt. Wie viele Zahlen man sich tatsächlich merken kann, hängt nicht nur von der individuellen Merkfähigkeit und den eventuell ablenkenden Umgebungsreizen ab, sondern auch von der Sprache. Chinesen kommen auf etwa neun Zahlen, die sie sich merken können – die Forscher führen dies aber nicht auf die höhere Merkfähigkeit zurück, sondern auf die Zahlnamen, die im Chinesischen wesentlich kürzer sind als z. B. im Deutschen (vgl. Dehaene 2011, S. 89).
Dieser Befund zeigt uns, dass die Eigenschaften der Darstellung auch dessen Verarbeitung beeinflussen. In diesem Fall betrifft die Verarbeitung die Aussprache der Darstellung. In anderen Fällen hingegen ist die Darstellung selbst bereits so unübersichtlich, dass sich die Darstellung nicht mehr gut als Wissensspeicher eignet und über die Zeit kaum noch benutzt wurde oder gar verloren gegangen ist.
Eine stark verkürzte Geschichte der Zahldarstellungen
Zu den ersten Zahldarstellungen gehörten Striche, die aneinander gereiht wurden. Doch schon nach kurzer Zeit wird diese Darstellung unübersichtlich und unpraktisch: Sie brauchen lange, um zu erkennen, dass ||||||||| die Zahl 9 darstellt. Eine einfache Abhilfe bietet eine Restrukturierung in Fünferblöcke, die es bei kleinen Zahlen schon deutlich vereinfacht, die Zahl zu erkennen. Doch der Vorteil dieser Restrukturierung bleibt letztendlich auf relativ kleine Zahlen beschränkt – bei der Zahl 132 sind Fünferblöcke wiederum ziemlich unübersichtlich und unpraktisch.
Es musste eine andere Darstellung für die Zahlen gefunden werden und es wurden viele neue entwickelt. Eine Darstellung, die uns bis heute noch relativ gut bekannt ist, sind die lateinischen Zahldarstellungen: I, II, III, IV, V, … Hier werden in regelmäßigen Abständen neue Buchstaben eingeführt, um die größer werdenden Zahlen nicht zu unübersichtlich werden zu lassen: X für 10, L für 50, C für 100, D für 500 usw. Das macht die Schreibweise für die Zahl 500 zwar außerordentlich kurz, aber gleichzeitig sind viel kleinere Zahlen wie XXXVII (37) bereits sehr unübersichtlich und es ist schwer, diese schnell zu erfassen. Neben diesem Nachteil braucht man außerdem immer wieder neue Zeichen, wenn man große Zahlen schreiben (und lesen) will. Alles in allem kostete diese römische Zahldarstellung immer noch zu viele kognitive Ressourcen, um sich durchzusetzen.
Durchgesetzt hat sich schließlich die indisch-arabische Zahldarstellung. Zu den zentralen Errungenschaften gehören hier ein konsequentes Stellenwertsystem und die Zahl 0. Das Stellenwertsystem bedeutet, dass z.B. die letzte 2 in 222 für zwei Einer steht, die mittlere dagegen für zwei Zehner und die vordere für zwei Hunderter. Anders als bei der römischen 37 oben hat die Stelle, an der die Ziffern stehen also immer eine Bedeutung, die jede Ziffer von den anderen unterscheidet. Dem liegt wiederum eine Menge von zehn verschiedenen Ziffern zugrunde, die in Kombination mit Zehnerpotenzen, also 1, 10, 100, … aber auch 0,1; 0,01; …, und einem Vorzeichen jede beliebige (rationale) Zahl darstellen können. So lässt sich 120,45 zerlegen in
\(1 \cdot 100 + 2 \cdot 10 + 0 \cdot 1 + 4 \cdot 0,1 + 5 \cdot 0,01.\)
Selbst große Zahlen lassen sich noch sehr übersichtlich und auf die immer gleiche Weise darstellen. Selbstverständlich hat auch dies irgendwann ein Ende, weil irgendwann zu viele Ziffern vorhanden sind, aber in diese Größenbereiche kommen wir selten (wenn es nicht gerade um die Staatsverschuldung geht). Zudem wächst die Unübersichtlichkeit, gemessen an der Anzahl der Ziffern, nur logarithmisch mit der Größe der Zahl.
Wichtig ist außerdem die Zahl 0. In früheren Darstellungen ließ man die Stellen, an die wir heute eine Null schreiben einfach frei, doch das führt schnell zu Verwirrung (ist das nun eine freie Stelle oder nur ein großer Zwischenraum?) und manche Zahlen lassen sich gar nicht unterscheiden (z.B. 1 und 10, 100, …). Die Null ermöglicht dagegen die klare Kennzeichnung des „Nichts“ und so natürlich uns diese Zahl heute vorkommt, so schwierig war es für unsere älteren Zeitgenossen, diese Zahl tatsächlich als Zahl zu akzeptieren, obwohl sie doch „Nichts“ bezeichnete.
Die indisch-arabische Zahldarstellung ermöglicht nicht nur eine übersichtliche Darstellung von Zahlen, sondern ebenfalls effiziente Schreibweisen für arithmetische Verfahren. Das erkennen Sie schnell an folgender Addition:
1238
+ 502
___1_
1740Diese Schreibweise funktioniert nur deshalb, weil Sie ein konsequentes Stellenwertsystem nutzen. Wenn Sie das gleiche mit den römischen Zahldarstellungen (MCCXXXVIII + DII) versuchen wollten, würde es nicht funktionieren.
Darstellungen verringern geistige Anstrengung: Funktion als impliziter Wissensspeicher
Wir können also feststellen, dass es eine Entwicklung der Zahldarstellungen gegeben hat, in deren Verlauf die Darstellung der Zahlen unseren kognitiven Ressourcen angepasst wurde, indem sich die Darstellungen, die effizienter zu verarbeiten waren und die effizientere Schreibweisen ermöglichten, gegenüber weniger effizienten Darstellungen durchsetzten (vgl. dazu auch Dehaene 2011).
Auf diese Weise fungieren die Darstellungen auch als impliziter Wissensspeicher. Kinder, die heute lernen mit den indisch-arabischen Zahldarstellungen umzugehen, müssen nicht mehr lernen, warum sich diese Darstellung durchgesetzt hat und warum sie besonders effizient zu verarbeiten ist. Sie können von den Errungenschaften ihrer mathematischen Vorgänger profitieren, indem sie einfach nur die gleichen Notationen verwenden.
Die Anpassung von Darstellungen an unsere kognitiven Möglichkeiten beschränkt sich im Übrigen nicht auf die Zahldarstellungen. Diese sind sogar ein relativ extremes Beispiel, weil sich die ganze Darstellungsart verändert. Häufig genügt es schon, einen Sachverhalt mit der gleichen Darstellungsart anders zu formulieren und damit anders darzustellen, damit der Sachverhalt kognitiv einfacher zu verarbeiten ist (also verständlicher wird). Das gilt auch für Sätze, die, wie Sie selbst wissen, schwierig oder einfach verständlich sein können, obwohl beide in derselben Schriftart und derselben Sprache geschrieben sind. Ein prominentes Beispiel aus der Mathematik ist die Differentialrechnung, die sowohl von Newton als auch von Leibniz erfunden wurde. Die beiden stellten ihre Überlegungen jedoch mit unterschiedlichen Notationen dar, sodass es zum (auch von den politischen Verhältnissen beeinflussten) „Wettstreit“ der Notationen kam. Durchgesetzt hat sich schließlich zum größten Teil die Notation von Leibniz, die effizientere Schreibweisen erlaubte, begrifflich klarer war und auf dem europäischen Kontinent weitere Verbreitung fand als die Notation von Newton, die sich nur auf der großbritannischen Insel eine Weile halten konnte.
Unterschiedliche Darstellungen als Repräsentanten desselben Sachverhalts
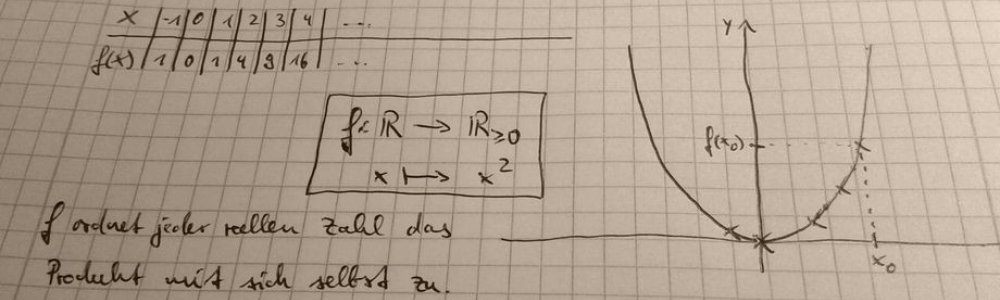
Für die Differentialrechnung und alle anderen modernen mathematischen Gebiete reichen die oben angesprochenen numerischen Darstellungen (also Darstellungen für Zahlen) natürlich nicht aus. Die Mathematiker haben verschiedene Darstellungsarten entwickelt, um über mathematische Sachverhalte nachzudenken. Das können Sie in der Abbildung unten gut am Beispiel einer quadratischen Funktion erkennen. Dadurch kann derselbe Sachverhalt auch durch unterschiedliche Zeichen dargestellt werden, die jeweils unterschiedliche Vor- und Nachteile haben, da sie unterschiedliche Aspekte betonen und unterschiedliche Zugänge bieten.
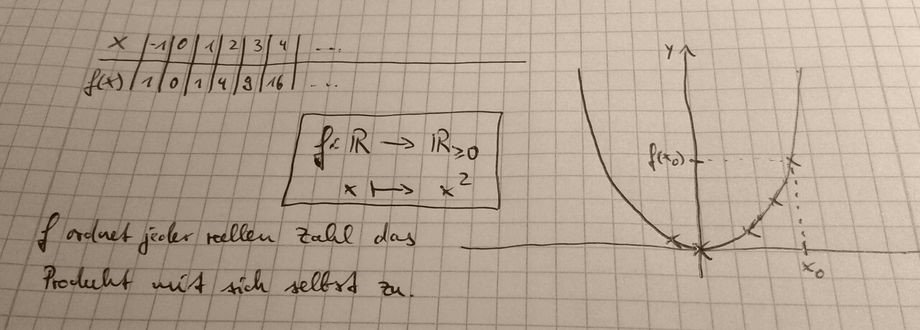
Es gibt unterschiedliche Kategorisierungen der vielen verschiedenen Darstellungsarten, die in der Mathematik verwendet werden. Eine recht einfache Unterscheidung bietet die Kategorisierung der Darstellungsart als Handlung, Bild, Zeichen oder Sprache (diese Einteilung wird in Kratz (2011), S. 136, beschrieben; angelehnt ist das an die klassische Einteilung von Jerome Bruner in enaktiv, ikonisch und symbolisch). Der Darstellung als Handlung kommt am Gymnasium und in der Wissenschaft Mathematik eine untergeordnete Rolle zu, weshalb ich diese hier ausklammern will. Die Sprache hingegen nimmt eine besondere Rolle ein. Weil sie, wie im letzten Artikel geschildert, weitgehend automatisch und mühelos verarbeitet wird, kann sie unterstützend mitwirken, wenn über bildliche oder formale („zeichenhafte“) Darstellungen gesprochen wird. Diese bildlichen und formalen Darstellungen bilden meist den Kern der mathematischen Darstellungen: Zahlen können mit den formalen indisch-arabischen Ziffern dargestellt werden oder als Punktmengen, Funktionen können durch eine formale Funktionsvorschrift oder durch einen Graphen dargestellt werden, für formale Terme gibt es ebenfalls Visualisierungen in Form von Flächeninhalten oder ähnlichem, der Satz des Pythagoras lässt sich unter der Voraussetzung, dass ein entsprechendes, rechtwinkliges Dreieck gegeben ist, mit \(a^2+b^2=c^2\) oder auch durch die Flächeninhalte der entsprechenden Quadrate an dem Dreieck darstellen. Es gibt noch viele Beispiele mehr, wie Graphen, Diagramme, Skizzen und Zeichnungen zur Visualisierung von formalen Zusammenhängen genutzt werden. Und dafür gibt es (mindestens) einen Grund.
Betrachten Sie das folgende Bild:
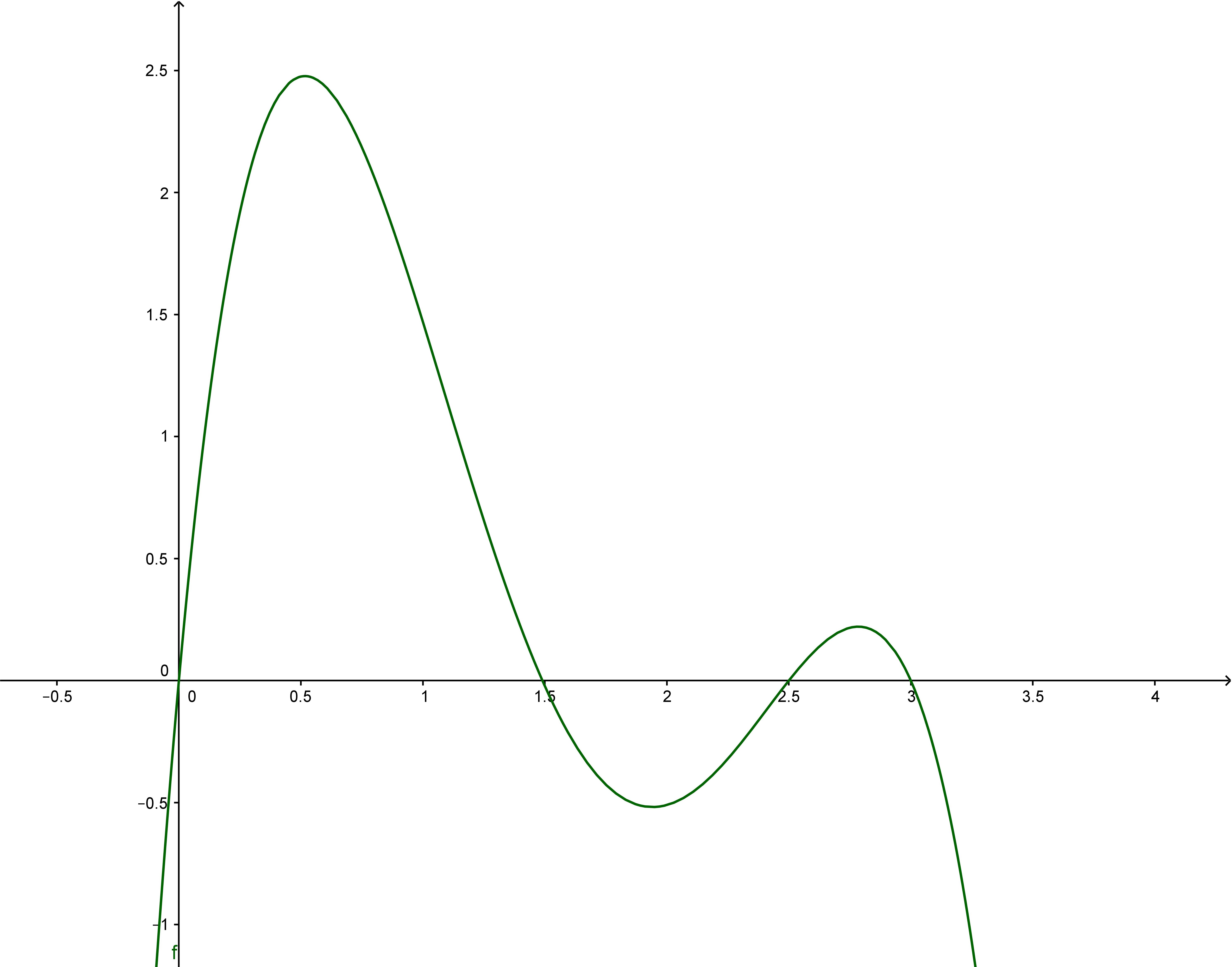
In dem Bild können Sie automatisch, schnell und mühelos erkennen, dass der Graph der abgebildeten Funktion einen höchsten Punkt hat und es erscheint Ihnen vollkommen einleuchtend, wenn man diesen Punkt als „Hochpunkt“ bezeichnet. Sie erkennen auch sofort, dass es noch einen zweiten Punkt gibt, der in einem bestimmten Bereich ebenfalls als (lokaler) Hochpunkt bezeichnet werden kann. Das beruht auf der visuell-räumlichen Wahrnehmung der Darstellung, wobei hier die Wahrnehmung von Abständen und Winkeln zwischen dem Graph und den Achsen gemeint ist und nicht die dreidimensionale Wahrnehmung, die aber an anderer Stelle auch dazu gehören kann. Diese visuell-räumliche Wahrnehmung ist eine Operation von System 1 und die Verwendung von bildlichen Darstellungen ermöglicht somit die Unterstützung des limitierten Systems 2 durch System 1. Und in diesem Fall handelt es sich tatsächlich um eine Unterstützung und keine Verzerrung, weil den Abständen zwischen dem Graphen und den Achsen ja tatsächlich eine Bedeutung zukommt. Daher ist die Visualisierung von Daten und formalen Zusammenhängen bis heute sowohl in der Schule als auch in der Wissenschaft ein wichtiger Schritt zum Verständnis der Sachverhalte. Wohl auch aus diesem Grund gehörte die Geometrie neben der Arithmetik zu den am frühesten entwickelten Themengebieten der Mathematik.
Dennoch reicht es nicht, auf dieser intuitiv zugänglichen, bildlichen Darstellungsebene zu bleiben, die uns so leicht verständlich scheint. Oder können Sie mir etwa die genauen Koordinaten der Hochpunkte nennen? Zu den Nachteilen von System 1 gehört, dass es in dieser Beziehung nicht sehr präzise arbeitet. Und zum Teil trügt es uns sogar. Sie haben im obigen Bild absolut keine Möglichkeit, zu erkennen, dass die zweite Nullstelle von links bei \(x=1,49\) liegt und nicht bei \(x=1,5\). Daher gehört es zu den schwierigen und komplizierten Schritten in der Schule und in der Wissenschaft, die bildlich erkannten Zusammenhänge oder Phänomene formal präzise zu erfassen, was notwendigerweise die Beteiligung von System 2 erfordert, wie wir schon im letzten Blogartikel gesehen haben. Das führt dann zu der formalen Übersetzung des optischen Eindrucks:
Sei \(f\) eine Funktion mit dem offenen Definitionsbereich \(D \subseteq \mathbb{R}\); außerdem sei \(h\) ein Element des Definitionsbereichs. Der Punkt \((h, f(h))\) heißt (lokaler) Hochpunkt, wenn es ein \(\epsilon >0\) gibt, sodass für alle \(x\) aus \(]h – \epsilon, h + \epsilon[\) gilt: \(f(x)<f(h)\).
Sie merken, dass Ihnen das Verständnis dieser Definition sehr viel mehr Mühe abverlangt und dass ihr Denken langsamer wird – Sie müssen Ihr System 2 aktivieren, um sie zu verstehen. Und das obwohl die Definition als Mischung aus verbaler und formaler Darstellung präsentiert ist. Zudem können Sie die explizite Benennung der Voraussetzungen sehen, die notwendig ist, um den zweiten Satz sinnvoll formulieren zu können. Das trägt zur Präzision und zum besseren Verständnis des Phänomens Hochpunkt bei, weil sehr viel mehr Eigenschaften bewusst gemacht werden müssen, aber es macht das Verständnis auch mühevoller. (Wenn Sie nicht alle Einzelheiten verstehen, ist das nicht schlimm. Hinter so einer Definition verstecken sich noch ein paar Hintergedanken, die ich hier nicht ausführlich ausbreiten möchte, weil die Definition auch so demonstriert, was ich beschrieben habe.)
Unterschiedliche Darstellungen für unterschiedliche kognitive Zugänge
So lassen sich die unterschiedlichen Darstellungen, die in der Mathematik heute benutzt werden, als Werkzeuge verstehen, die eine lange Entwicklung zur Steigerung der Effizienz bei der kognitiven Verarbeitung hinter sich haben. Das betrifft sowohl die Darstellungsart als auch die jeweilige Formulierung mit einer bestimmten Darstellungsart. Dabei hat jede der verschiedenen Darstellungsarten andere kognitive „Verarbeitungskanäle“ angesprochen und wurde für diese weiterentwickelt. So sprechen bildliche Darstellungen unter anderem die visuell-räumliche Wahrnehmung (System 1) an, während formale Darstellungen die bewusste Verarbeitung (System 2) erfordern und dadurch Präzision ermöglichen. Insbesondere gibt es aber keine so klare Trennung wie im letzten Artikel angedeutet, dass nur System 2 Mathematik betreiben kann, auch wenn ein großer Teil der Mathematik (heute) in formaler Darstellung repräsentiert wird. Durch bildliche (und auch sprachliche) Darstellungen verschaffen die Mathematiker immer wieder ihrem System 1 Zugang zur Mathematik und eröffnen dadurch die Möglichkeit, die unglaublich großen Kapazitäten von System 1 anzuzapfen. Durch die geeignete Zerlegung und Darstellung von Problemen lässt sich die notwendige geistige Anstrengung und Aufmerksamkeitsfokussierung auf ein Maß herunterbrechen, das uns die Lösung des Problems erst ermöglicht.
Für die Schule bedeuten die verschiedenen Verarbeitungsmöglichkeiten der Darstellungen, dass die Schüler in der Regel zuerst mit einer bildlichen Darstellung von Zusammenhängen vertraut gemacht werden sollten, weil diese sich einfacher verarbeiten lässt und ein erstes Grundverständnis ermöglicht. Erst danach sollte der Übergang zur formalen Darstellung folgen und dieser muss langsam stattfinden, um die begrenzten Ressourcen von System 2 nicht zu überlasten. Wichtig ist aber auch, dass dieser Übergang nicht ausgelassen werden darf, weil sonst die Präzision der formalen Darstellung nie erreicht wird. Sowohl die bildlichen als auch die formalen Darstellungen sollten stets von Verbalisierungen begleitet werden, also um einen dritten, sprachlichen Zugang ergänzt werden. Zu guter Letzt müssen die Schüler in die Lage versetzt werden, flexibel zwischen den Darstellungsarten hin und her zu wechseln, um sich selbst den für sie besten Zugang zu den Problemen zu verschaffen, die sie lösen wollen. Diese Forderungen sind im Übrigen nicht neu, sondern lange bekannt (sie sind z.B. auch bei Kratz 2011 beschrieben). Ich habe Sie hier lediglich in Zusammenhang mit den Denksystemen gebracht, die ich im letzten Artikel beschrieben habe.
Moderne Darstellungen
Am Ende dieses Artikels möchte ich noch darauf aufmerksam machen, dass wir ganz sicher nicht am Ende der Entwicklung der Darstellungen für die Mathematik stehen. Die sprachliche Darstellung war eine der oben erwähnten Darstellungsarten und ich denke, dass man darunter nicht nur unsere Muttersprache, nicht einmal nur die gesprochenen Sprachen verstehen sollte. Unsere Zeit wird geprägt von den Umbrüchen, die Programmiersprachen uns ermöglichen und diese werden unter anderem genutzt, um mathematische Formeln und Verfahren auszudrücken. Auch wenn wir noch nicht besonders viel darüber wissen, gehen wir davon aus, dass verschiedene gesprochene Sprachen unser Denken auch über Mathematik beeinflussen. Und dasselbe sollten wir annehmen, wenn wir mithilfe von Programmiersprachen über Mathematik nachdenken und Mathematik darstellen. Wie die verschiedenen Sprachen unser Denken beeinflussen, ist jedoch noch völlig unerforscht.
Quellen
Dehaene, Stanislas (2011): The Number Sense. How the Mind creates Mathematics. Revised and Updated Edition. Oxford University Press.
Kahneman, Daniel (2015): Schnelles Denken, langsames Denken. 14. Auflage. Pantheon-Ausgabe.
Kratz, Henrik (2011): Wege zu einem kompetenzorientierten Unterricht. 1. Auflage. Kallmeyer in Verbindung mit Klett.